最小二乗法メモ

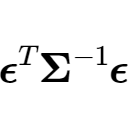
この記事の目的

最小二乗法はとても広く使われていて解説も多数存在しますが、線形空間のみなど簡単な場合についてしか書かれていないことが多いです。より一般化した問題（例えば、3次元回転をパラメーターにもつとき）に適用しようとすると資料が少ないです。この記事では自分の整理用に、より一般化した最小二乗法について記述します。また、なるべく違う文脈で同じ変数を使わないようにし、変数がどんな集合の元なのか、写像の定義域と値域を明記することを心がけます。

なお、私は数学の専門家ではないので、用語や記号の使い方が間違っていたり主張に必要な条件を見落としている可能性があります。

数式の表記

ベクトルは列ベクトルとして行列とともにbold italicで表記します。Lie群またはその元はカリグラフィーフォントで表記します。微分は分子レイアウト（numerator-layout）とします。

Lie群に関連する表記はSola2018にならいます。この文書では$\oplus$を$\textrm{right-}\oplus$、$\ominus$を$\textrm{right-}\ominus$として説明しますが、leftに読み替えることもできます。

最小二乗法とは

誤差を含む互いに独立な観測値$\{ \overline{\mathcal{Z_i}} \mid \overline{\mathcal{Z_i}} \in \mathcal{N_i} \}$が得られたとき、パラメーター$\mathcal{X} \in \mathcal{M}$をもつ観測に対応する予測モデル$f_i: \mathcal{M} \to \mathcal{N_i}$を考えます。ここで、$\{ \mathcal{N_i} \}$と$\mathcal{M}$はLie群とします。$\mathcal{N_i}$の接ベクトル空間の基底の数を$n_i$、$\mathcal{M}$の接ベクトル空間の基底の数を$m$とします。

最小二乗法では、モデルを使った予測値と観測値$\overline{\mathcal{Z_i}}$の間に以下のノイズモデルを仮定します。 \[ \overline{\mathcal{Z_i}} = f_i(\mathcal{X}) \oplus \vect{\epsilon_i},\ \vect{\epsilon_i} \sim N(\vect{0}, \vect{\Sigma_i}) \] $\vect{\Sigma_i}$は既知とし、$\vect{\epsilon_i}$は互いに独立とします。$\vect{\epsilon_i}$は残差（residual）とも呼ばれます。$\vect{\epsilon_i}$を$\mathcal{X}$の関数として書くと次のようになります。 \[ \vect{\epsilon_i}: \mathcal{M} \to T_{\mathcal{Z_i}(\mathcal{X})}\mathcal{N_i} = \mathbb{R}^{n_i},\ \vect{\epsilon_i}(\mathcal{X}) := \overline{\mathcal{Z_i}} \ominus f_i(\mathcal{X}) \] この残差の重み付き二乗和を最小化するパラメーターを求めるのが最小二乗法です。 \[ \hat{\mathcal{X}} = \argmin_\mathcal{X} \sum_i \frac{1}{2} {\vect{\epsilon_i}(\mathcal{X})}^T \vect{\Sigma_i}^{-1} \vect{\epsilon_i}(\mathcal{X}) \]

ここで、各観測の直積で新たなLie群$\mathcal{N} := \prod_i \mathcal{N_i}$を定義し、$\overline{\mathcal{Z}}$も定義します。 \[ \overline{\mathcal{Z}} := (\cdots, \overline{\mathcal{Z_i}}, \cdots) \in \mathcal{N} \] 同様にモデルも定義します。 \[ f: \mathcal{M} \to \mathcal{N},\ f(\mathcal{X}) := (\cdots, f_i(\mathcal{X}), \cdots) \] $\overline{\mathcal{Z}}$と$f$の関係は残差$\vect{\epsilon}$を使って以下のようになります。 \[ \overline{\mathcal{Z}} = f(\mathcal{X}) \oplus \vect{\epsilon} \] \[ \vect{\epsilon} \sim N(\vect{0}, \vect{\Sigma}) \label{noise-model} \] \[ \vect{\Sigma} := \begin{bmatrix} \ddots & & \vect{0} \\ & \vect{\Sigma_i} & \\ \vect{0} & & \ddots \end{bmatrix} \in \mathbb{R}^{n \times n} \] \[ n := \sum_i n_i \] 以上の新たに定義した残差を使った最小二乗法は \[ \vect{\epsilon}: \mathcal{M} \to T_{\mathcal{Z}(\mathcal{X})}\mathcal{N} = \mathbb{R}^n,\ \vect{\epsilon}(\mathcal{X}) = \overline{\mathcal{Z}} \ominus \mathcal{Z}(\mathcal{X}) \] \[ \hat{\mathcal{X}} = \argmin_\mathcal{X} \frac{1}{2} {\vect{\epsilon}(\mathcal{X})}^T \vect\Sigma^{-1} \vect{\epsilon}(\mathcal{X}) \label{leastsq} \] と簡潔に書けます。 $\vect\Sigma$はブロック対角行列なので、その逆行列は各ブロックの逆行列を並べたブロック対角行列になります。 \[ \vect{\Sigma}^{-1} = \begin{bmatrix} \ddots & & \vect{0} \\ & \vect{\Sigma_i}^{-1} & \\ \vect{0} & & \ddots \end{bmatrix} \in \mathbb{R}^{n \times n} \]

重みなし最小二乗法は$\vect\Sigma$を単位行列とした特殊な場合として扱うことができます。

係数の$\frac{1}{2}$は便宜上つけているだけで、本質的な意味はないです（最小化する目的関数に任意の正の定数をかけても結果は変わりません）。目的関数を微分したとき、出てくる係数2と打ち消しあって式が簡潔になるといった効果があります。

また、${\vect{\epsilon}(\mathcal{X})}^T \vect\Sigma^{-1} \vect{\epsilon}(\mathcal{X})$の部分に注目すると、これは$\vect{\epsilon}$のマハラノビス距離の二乗になっています。つまり、最小二乗法はマハラノビス距離の二乗和の最小化ととらえることもできます。

最尤推定との関係

$\eqref{leastsq}$の式の形になる理論的背景には最尤推定（MLE）があります。あるパラメーターが与えられたときの残差の確率密度関数は$\eqref{noise-model}$から次のようになります。 \[ p(\vect{\epsilon} \mid \mathcal{X}) = N(\vect{0}, \vect{\Sigma}) = (2\pi)^{-\frac{n}{2}} |\vect{\Sigma}|^{-\frac{1}{2}} \exp\left( -\frac{1}{2} {\vect{\epsilon}(\mathcal{X})}^T \vect\Sigma^{-1} \vect{\epsilon}(\mathcal{X}) \right) \] 残差が得られたときのパラメーターの尤度は次のようになります。 \[ L(\mathcal{X} \mid \vect{\epsilon}) = p(\vect{\epsilon} \mid \mathcal{X}) \] さらに対数尤度を考える次のようになります。 \begin{align} l(\mathcal{X} \mid \vect{\epsilon}) &= \log L(\mathcal{X} \mid \vect{\epsilon}) \\ &= -\frac{n}{2}\log{2\pi} -\frac{1}{2} \log|\vect{\Sigma}| -\frac{1}{2} {\vect{\epsilon}(\mathcal{X})}^T \vect\Sigma^{-1} \vect{\epsilon}(\mathcal{X}) \end{align} 尤度を最大化するパラメーターを考えます。 \begin{align} \hat{\mathcal{X}} &= \argmax_\mathcal{X} L(\mathcal{X} \mid \vect{\epsilon}) \\ &= \argmax_\mathcal{X} l(\mathcal{X} \mid \vect{\epsilon}) \\ &= \argmin_\mathcal{X} -l(\mathcal{X} \mid \vect{\epsilon}) \\ &= \argmin_\mathcal{X} \left( \frac{n}{2}\log{2\pi} +\frac{1}{2} \log|\vect{\Sigma}| +\frac{1}{2} \vect{\epsilon}(\mathcal{X})^T \vect\Sigma^{-1} \vect{\epsilon}(\mathcal{X}) \right) \\ &= \argmin_\mathcal{X} \frac{1}{2} {\vect{\epsilon}(\mathcal{X})}^T \vect\Sigma^{-1} \vect{\epsilon}(\mathcal{X}) \label{mle} \end{align} 以上のように$\eqref{leastsq}$と$\eqref{mle}$が一致し、最小二乗法は残差が平均0の多変量正規分布に従うと仮定した最尤推定量に一致することが確認できました。

実用上の話

以上の議論で最小二乗法が置いている仮定がいくつか出てきました。

• 各観測は独立
• 残差の分散が既知
• 残差が平均0の正規分布に従う

実際は残差の分布や分散を正確に知ることは困難な場合がほとんどなので、正規分布で近似できるとしてしまって分散は適当に決めた正定値行列にすることが多いです。もっと簡単にして適当な正の定数を並べた対角行列もよく使われます。また、最小化する関数に正の定数をかけてもパラメーターの推定値は変わらないため、分散の全体のスケールは不定でもよいです（相対比がわかっていれば十分）。

ただし注意点は、残差が正規分布からあまりにもかけ離れた分布をしている場合や分散を適切に設定しない場合、求めた推定量は最尤推定量でもなんでもないので、ほぼ意味のない値になります。ノイズの特性がわかっていない問題に対しては、データから残差を計算してプロットした上で分布や分散の異方性を確認し、正規分布で近似できるのか確認してから適用したほうがいいでしょう。とりあえずなんでも最小二乗法を使えばいいというわけではありません。

また、あくまでも最尤推定量なので、そもそも最尤推定が適さない問題に対してはベイズ推定などほかの枠組みを用いる必要があります。

最小二乗法の解法

モデルが線形関数の場合は多くの解説があるので、ここでは非線形の場合について記します。 非線形最小二乗法に対する閉じた形で書ける解は一般にはなく、ほとんどの場合反復法で数値的に解きます¹。具体的にはガウス・ニュートン法とその派生のレベンバーグ・マーカート法（修正ガウス・ニュートン法）がよく使われます²。ここでは詳細は他の文献に譲り、Lie群に拡張した上で概要を記述します。

ガウス・ニュートン法

\[ \label{energy} E(\mathcal{X}) := \frac{1}{2} {\vect{\epsilon}(\mathcal{X})}^T \vect\Sigma^{-1} \vect{\epsilon}(\mathcal{X}) \in \mathbb{R} \] とおきます。さらに、滑らかであるとします。パラメーターを現在の推定値$\mathcal{X_k} \in \mathcal{M}$で固定し、その接ベクトル空間にそってステップ幅${}^{\mathcal{X_k}}\vect\tau \in T_{\mathcal{X_k}}\mathcal{M} = \mathbb{R}^m$だけ動かして$E(\cdot)$を最小化するステップ幅${}^{\mathcal{X_k}}\hat{\vect\tau}$を考えます。 \[ {}^{\mathcal{X_k}}\hat{\vect\tau} = \argmin_{{}^{\mathcal{X_k}}\vect\tau} E(\mathcal{X_k} \oplus {}^{\mathcal{X_k}}\vect\tau) \] ガウス・ニュートン法では$\vect\epsilon(\cdot)$を次のように近似します（Sola2018 式43を参照）。 \begin{align} \def\r{{\vect{\epsilon}(\mathcal{X})}} \def\j{{\vect{J}(\mathcal{X})}} \def\d{{{}^{\mathcal{X}}\vect\tau}} \vect\epsilon(\mathcal{X} \oplus {}^{\mathcal{X}}\vect\tau) \simeq \r+\j\d \label{gnapprox} \\ \vect{J}(\mathcal{X}) := \frac{{}^{\mathcal{X}}D\vect\epsilon(\mathcal{X})}{D\mathcal{X}} \in \mathbb{R}^{n \times m} \end{align} $\eqref{gnapprox}$を$\eqref{energy}$に代入して${}^{\mathcal{X}}\vect\tau$の関数として定義し直します。 \[ \def\r{{\vect{\epsilon}(\mathcal{X})}} \def\j{{\vect{J}(\mathcal{X})}} \def\d{{{}^{\mathcal{X}}\vect\tau}} E_\mathcal{X}({}^{\mathcal{X}}\vect\tau) := \frac{1}{2} (\r+\j\d)^T \vect\Sigma^{-1} (\r+\j\d) \in \mathbb{R} \] ステップ幅は次のようになります。 \[ \label{gnstep} {}^{\mathcal{X_k}}\hat{\vect\tau} = \argmin_{{}^{\mathcal{X_k}}\vect\tau} E_\mathcal{X_k}({}^{\mathcal{X_k}}\vect\tau) \]

$\vect\Sigma^{-1}$は分散共分散行列の逆行列なので、対称行列かつ半正定値行列です。したがって$E_\mathcal{X}({}^{\mathcal{X}}\vect\tau)$は凸関数なので、最小値は極小値と一致し、極小値をとるのは1階微分が0になるときです。つまり$\eqref{gnstep}$は次の問題に置き換えられます。 \[ \label{gneq} \def\t{{{}^{\mathcal{X_k}}\vect\tau}} \def\ht{{{}^{\mathcal{X_k}}\hat{\vect\tau}}} \left. \frac{\partial E_\mathcal{X_k}({}^{\mathcal{X_k}}\vect\tau)}{\partial \t} \right|_{\t=\ht} = \vect{0} \] 展開して整理すると次の線形方程式を得ます。 \[ \def\j{{\vect{J}(\mathcal{X_k})}} \def\w{{\vect\Sigma^{-1}}} \def\t{{{}^{\mathcal{X_k}}\hat{\vect\tau}}} \def\r{{\vect{\epsilon}(\mathcal{X_k})}} \j^T \w \j \t = -\j^T \w \r \] 正規方程式と呼ばれるもので、コレスキー分解・QR分解・特異値分解などの行列分解を用いて解くことができます。そして、得られたステップ幅でパラメーターを更新します。 \[ \mathcal{X_{k+1}} = \mathcal{X_k} \oplus {}^{\mathcal{X_k}}\hat{\vect\tau} \] これを適当な収束条件を満たすまで繰り返すのがガウス・ニュートン法です。

実際は解から遠いときに数値的に不安定になったり収束性が悪い、収束が保証されていないなど実用的ではないので、これに改良を加えたレベンバーグ・マーカート法を用いることが多いです。

次の記事「ガウス・ニュートン法の実装」では、具体例としてパラメーターが線形空間と$SO(3)$の場合をPythonで実装して説明しています。